Обзор объектива Sigma 50mm f1.4 DG HSM Art. Реальная альтернатива Canon EF 50mm f1.2 L USM

Отличия между L1 и L2-регуляризациями

Сейчас  мы рассмотрим отличия между L1 и L2-регуляризациями и покажем, как эти отличия появляются вследствие математических выкладок. Мы начнем сразу с различий, а затем объясню, вследствие чего они возникают.

Мы уже видели, что L1-регуляризация способствует разреженности функции, когда лишь немногие факторы не равны нулю. L2-регуляризация способствует появлению малых весовых коэффициентов модели, но не способствует их точному равенству нулю.

Предлагаем  обсудить, почему так получается.

L1-регуляризация реализует это путём отбора наиболее важных факторов, которые сильнее всего влияют на результат. Для простоты можете считать, что факторы с малой величиной влияния на конечный результат фактически «помогают» вам предсказывать лишь шум в наборе обучающих данных.

L2-регуляризация предотвращает переобученность модели путём запрета на непропорционально большие весовые коэффициенты.Для начала пройдёмся по уже существующим и использующимся методикам. Их стоит изучить, поскольку мы считаем, что они неадекватны и отвлекают много ресурсов. Контурный график отрицательных логарифмов показывает различия между каждым из типов регуляризации, и хотя это и не слишком полезно для понимания сути, будет замечательно, если вы его изучите.Что на самом деле полезно – представить себе модель с одномерным весовым коэффициентом. При L2-регуляризации дополнительный член является квадратичной функцией, при L1-регуляризации – модулем

Что здесь действительно важно – производная функции. Производная, конечно, является ключевой, поскольку градиентный спуск в основном движется в направлении производной.При квадратичном члене чем ближе вы находитесь к нулю, тем меньшей становится ваша производная, пока также не приблизится к нулю

Поэтому при L2-регуляризации когда ваша величина w уже мала, дальнейший градиентный спуск уже её сильно не изменит. В случае модуля производная является константой с абсолютной величиной, равной единице. Формально в нуле она не определена, но мы считаем её также равной нулю.Поэтому при L1-регуляризации градиентный спуск будет стремиться к нулю с постоянной скоростью, а достигнув его, там и останется. Вследствие этого L2-регуляризация способствует малой величине весовых коэффициентов, а L1-регуляризация способствует их равенству нулю, тем самым провоцируя разрежённость.Такая модель даже имеет специальное название – ElasticNet. Звучит, конечно, довольно причудливо, но на самом деле это просто добавление и штрафа L1-регуляризации, и штрафа L2-регуляризации к вашей функции затрат.
JRIDGE = J + λ2|w|2,
JLASSO = J +λ1|w|,
JELASTICNET = J + λ1|w| + λ2|w|2.

Post Views:
13 630

Обучение бойцов

При поражении осколками гранаты велика доля случайности: так, в некоторых случаях подрыв гранаты в непосредственной близости от бойца может только оглушить его; однако известны случаи, когда одиночный осколок гранаты поражал бойца, находящегося в укрытии на дистанции 70-80 метров от места подрыва гранаты.

Для новобранцев метание гранаты часто представляет психологическую проблему: основываясь на представлениях, полученных из боевиков, они считают гранату оружием чудовищной разрушительной силы и испытывают панический страх, что приводит к глупым и абсурдным действиям, которые действительно могут представлять угрозу их жизни. Так, например, они могут метнуть вместо гранаты чеку, а гранату оставить в окопе; уронить активированную гранату себе под ноги и, будучи парализованными страхом, стоять, дожидаясь взрыва, вместо того, чтобы отбежать и залечь

Также важно соблюдать технику безопасности при метании гранат в зимнее время: граната при броске может зацепиться за торчащие части одежды и полететь в опасном для бойца направлении, или даже закатиться в рукав.

Примечания

1. Вернидуб И. И. Ручные гранаты — «карманная» артиллерия пехоты // Боеприпасы победы. Очерки. — Москва: ЦНИИНТИКПК, 1998. — С. 95. — 200 с.
2. Наставление по стрелковому делу. Ручные гранаты. — М.: Военное издательство Министерства обороны СССР. 1965 — 65, стр.15
3. ↑ Б. В. Прибылов, Е. Н. Кравченко. Ручные и ружейные гранаты. — М.: «Арктика 4Д», 2008. — 776
4. Краткое описание устройства и применения ручных гранат марки Ф-1 с запалом системы Ф. В. Ковешникова. Артиллерийское Управление РККА. М. 1937 г.
5. А. А. Благонравов, М. В. Гуревич. Боеприпасы стрелкового вооружения. Патроны, ручные и ружейные гранаты. Их устройство. Л.: Издание военно-технической академии РККА имени тов. Дзержинского, 1932 г., стр. 159
6. ↑ Федосеев С. Л. Метательные снаряды советской пехоты. Военно-промышленный курьер. Выпуск № 39 (355) за 6 октября 2010 г.
7. ↑
8. Очень часто при описании этого типа боеприпасов указывается расстояние 200 м. Теоретически осколки гранаты могут улететь на такое расстояние, однако вероятность попадания этих осколков в цель стремится к нулю. Скорее всего, под дистанцией в 200 м понимается расстояние, на котором должен находиться наблюдатель для того, чтобы ни при каких условиях не получить ранение. В реальности о более-менее гарантированном поражении стоящего в рост человека можно говорить на дистанции не более 5—10 метров. На дистанциях более 50 м поражение человека крайне маловероятно
9. ↑
10. Опасными считаются осколки массой не менее 2 грамм. Осколки меньшей массы, даже обладая большой скоростью, не в состоянии причинить сколь нибудь значительных повреждений. Таким образом, теоретически одна граната массой 540 г (масса заряда взрывчатого вещества 60 г) при идеальных условиях может дать до 270 осколков, обладающих убойным действием. В реальности количество и масса осколков колеблются в очень больших пределах, и число убойных осколков не превышает 150—200. В случае, если граната взрывается на земле, число убойных осколков уменьшается примерно вдвое, так как осколки, уходящие в нижнюю полусферу, не представляют опасности
11. ↑
12. ↑
13. Журнал «Оружие» № 8 за 1999 г., статья «Подготовить гранаты»
14. ↑

Оценка проекта

В целом, данный образец противопехотной гранаты следует считать удачным. Ф-1 прошла проверку временем, имеет простое, надёжное устройство, технологична и проста в изготовлении, эффективно справляется с поставленными перед данным типом оружия задачами. Закономерно, что недостатки проекта вытекают из его достоинств.

Достоинства

Благодаря своей простой и надёжной конструкции граната Ф-1 состоит на вооружении уже около 70 лет без существенных изменений и, вероятно, ещё долго не будет снята с вооружения. Достоинства, обеспечивающие такой долгий срок службы, следующие:

• Корпус естественного дробления, из которого успешно формируются поражающие элементы даже при повреждениях металлической рубашки.
• Дистанционный запал обладает относительно простой конструкцией и отличается высокой надёжностью.
• Цельнометаллический монолитный корпус прост в изготовлении и может быть изготовлен практически на любом промышленном предприятии, даже не специализированном. Материал корпуса — сталистый чугун — очень дёшев.
• Простота внутренней конструкции позволяет в условиях войны использовать вместо штатного тротила любую имеющуюся в распоряжении взрывчатку.
• Мощность взрыва данной гранаты такова, что, будучи брошенной в колодец, буквально «выбрасывает» все находящиеся в нём предметы, включая воду. Это свойство полезно при штурмах различных шахт и тоннелей среднего диаметра. Если скрывающегося за поворотом, углом или иным препятствием на дистанции ближе 30 метров от взрыва противника не заденут осколки, то его почти гарантированно убьёт резким пневматическим ударом, вызванным взрывной волной. Атакующему при этом запрещено находиться в туннеле, так как он сам может пострадать.
• Дистанционное действие подрыва позволяет забрасывать гранату к противнику, используя отскок от стен, потолка и различных препятствий.

Недостатки

Недостатки данной гранаты обусловлены преимущественно устареванием её конструкции, а не недочётами при конструировании. К ним относятся:

• Низкая эффективность образования осколков при дроблении корпуса. Большая часть массы корпуса (до 60 %) образует слишком мелкие неубойные осколки. В то же время, часто образуется и несколько слишком крупных осколков, повышающих опасную дистанцию и снижающих число осколков оптимального размера. Рифление корпуса, имеющее, в общем, случайный характер, не может обеспечить формирование осколков удовлетворительной формы и оптимальное распределение их по массе (сама идея формирования осколков предсказуемого размера за счёт рифления корпуса оказалась не совсем верной).
• Дистанционный запал не приводит к взрыву при попадании в цель, а срабатывает через некоторое время (это свойство любого дистанционного запала, а не только УЗРГ).
• Граната относительно тяжёлая, что несколько снижает предельную дальность броска.

L2-регуляризация. Код

Начнём с импорта библиотек NumPy и Matplotlib.

import numpy as np

import matplotlib as plt

Установим количество опытов равным 50. Сгенерируем данные таким образом, чтобы у нас было 50 точек, равномерно распределённых между 0 и 10. Установим Y=0,5x плюс некоторый случайный шум.

N = 50.

X = np.linspace(0, 10, N)

Y = 0.5X + np.random.randn(N)

Теперь вручную создадим пару «холмов». Установим значение первой конечной точки на 30 больше, чем она есть, и значение второй конечной точки тоже на 30 больше, чем она есть.

Y += 30

Y += 30

Следующее – изобразим наши данные графически. Вы уже знаете, как это делается.

plt.scatter(X, Y)

plt.show()

Теперь найдём решение для весовых коэффициентов. Добавим условия смещения.

X = np.vstack().T

И найдём максимум функции правдоподобия. Назовём эту переменную w_ml. Вы уже знаете, как его вычислять. Сразу же изобразим графически оригинальные данные и максимум функции правдоподобия.

w_ml = np.linalg.solve(X.T.dot(X), X.T.dot(Y))

Yhat_ml = X.dot(w_ml)

plt.scatter(X, Y)

plt.plot(X, Yhat_ml)

plt.show()

Теперь найдём решение для L2-регуляризации. Установим штраф, равным 1000 и снова отобразим результат графически.

l2 = 1000.0

w_map = np.linalg.solve(l2*np.eye(2) + X.T.dot(X), X.T.dot(Y))

Yhat_map = X.dot(w_map)

plt.scatter(X, Y)

plt.plot(X, Yhat_ml, label=’maximum likehood’)

plt.plot(X, Yhat_map, label=’map’)

plt.legend()

plt.show()

Теперь запустим программу и посмотрим, что получилось.

На первой диаграмме наши входные данные с нашим «холмом».

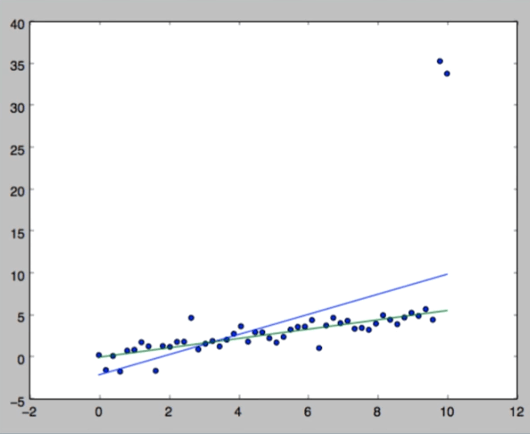
На второй диаграмме изображено решение для максимума функции максимального правдоподобия.

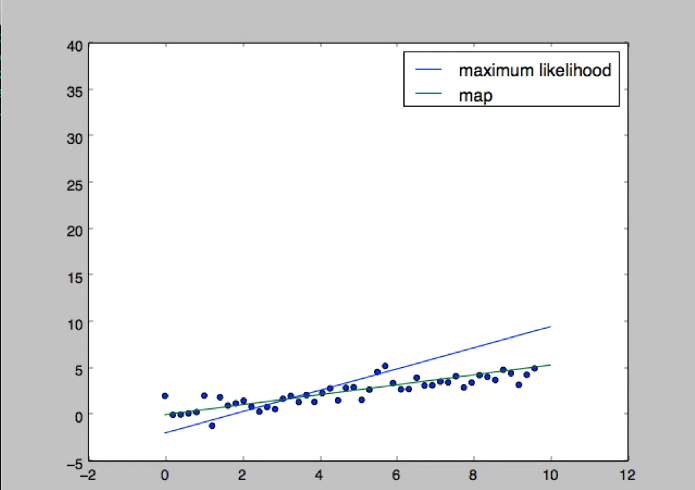
Заметьте, что оно не очень удачно, так как тянется к «холму». Теперь посмотрим решение для максимизации апостериора и решение для максимального правдоподобия вместе

Обратите внимание, что МАР соответствует тенденции намного больше, чем функция максимального правдоподобия

Что такое L2 регуляризация в машинном обучении Теория

И так сейчас мы с вами обсудим методику, известную как L2-регуляризация, помогающая решить проблему переобученности модели. Суть в том, что чересчур тяжёлые весовые коэффициенты «отталкивают» нашу линию наилучшего соответствия, построенную на основе минимизации квадрата ошибок, от основной тендеции.

На графике вы видите, как линия наилучшего соответствия, построенная с помощью L2-регуляризации, куда лучше описывает основную тенденцию, чем линия, построенная на основе минимизации квадрата ошибок.

 Как же работает L2-регуляризация?

Суть состоит в том, что мы изменяем нашу первоначальную функцию, добавляя «штраф» на большие весовые коэффициенты. Для этого мы добавляем постоянную , умноженный на квадрат w

Пока что всё довольно просто.

Посмотрим теперь на эту проблему с точки зрения вероятности. Вначале мы искали максимум функции правдоподобия, но теперь, когда мы изменили нашу функцию ошибок, это уже не работает. Мы знаем, что квадрат ошибок эквивалентен минимуму отрицательного логарифма функции правдоподобия, что эквивалентно максимуму функции правдоподобия. Экспонируем нашу новую функцию издержек.

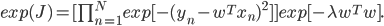
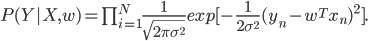
Мы видим два гауссиана. Первый – тот же, что и был прежде. Второй гауссиан новый. В нём w является случайной величиной со средним значением, равным нулю, и дисперсией, равно единица на лямбду. Этот второй гауссиан мы называем приором. Он описывает w независимо от данных, так как, как легко убедиться, он не зависит от X или Y.

Вы можете здесь узнать правило Байеса. Действительно,

P(w|Y,X) называется апостериором, а этот метод – методом максимизации апостериора, сокращённо MAP. Это значит, что теперь мы ищем максимум апостериора, а не функции правдоподобия, как ранее.

Итак, теперь, когда мы разобрали некоторые теоретические основы L2-регуляризации, как же нам найти w? Точно так же, как и ранее – берём производную нашей новой функции затрат, приравниваем её к нулю и решаем относительно w. Прежде всего выпишем нашу функцию затрат в полной матричной форме.

J = (Y – Xw)T(Y – Xw) + λwTw,

J = YTY – 2YTXw + wTXTXw + λwTw.

Затем берём производную и приравниваем к нулю:

И решаем полученное уравнение относительно w.

(λI + XTX)w = XTY,

w = (λI + XTX)-1XTY

Наш результат аналогичен прежнему, за исключением наличия λ.

Подведём итоги. Одним из способов избежать переусложнения модели и её переобученности является L2-регуляризация, также известная под названием регрессии Риджа. Работает она так. Мы добавляем квадрат величины весовых коэффициентов, умноженный на константу λ, к нашей прежней квадратической функции погрешностей. Мы делаем это потому, что большое значение весовых коэффициентов являются признаком переобученности. Далее мы решаем уравнение относительно w, беря производную и приравнивая её к нулю. Это и есть метод максимизации апостериора (MAP), так как мы находим максимум апостериора w для данных

Использование

Для применения гранаты необходимо разогнуть усики предохранительной чеки, взять гранату в правую руку так, чтобы пальцы прижимали рычаг к корпусу. Перед метанием гранаты, продев указательный палец левой руки в кольцо чеки, выдернуть её. Опытные инструкторы утверждают, что левша без проблем может держать и метать гранату левой, а чеку выдёргивать правой. Граната может продолжать оставаться в руке сколько угодно долго, пока не отпущен рычаг, ударник запала не может разбить капсюль (в принципе, если потребность в броске гранаты отпала, а чека не выброшена, её можно (не отпуская рычаг!) вставить обратно; после загибания усиков чеки граната пригодна к нормальному хранению).[источник не указан 648 дней] После выбора момента броска и цели — бросить в цель гранату. В этот момент рычаг под воздействием пружины ударника повернётся, освобождая ударник, и отлетит в сторону. Ударник наколет капсюль и через 3,2 — 4,2 секунды произойдёт взрыв.

Граната предназначена для поражения живой силы и небронированной техники. Поражающими факторами являются непосредственное фугасное действие взрывчатки и осколки, формирующиеся при разрушении металлической оболочки гранаты.