Число 15, 0x00000F, пятнадцать

История

В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.

Лука Пачоли, современник и друг Леонардо да Винчи, усматривал в этом отношении «божественную суть», выражающую триединство Бога Отца, Сына и Святого Духа.

Неизвестно точно, кто и когда именно впервые ввел в обращение термин «золотое сечение». Несмотря на то, что некоторые авторитетные авторы связывают появление этого термина с Леонардо да Винчи в XV веке или относят появление этого термина к XVI веку, самое раннее употребление этого термина находится у Мартина Ома в 1835 году в примечании ко второму изданию его книги «Чистая элементарная математика», в котором Ом пишет, что это сечение часто называют золотым сечением (нем. goldener Schnitt). Из текста примечания Ома следует, что Ом не придумал этот термин сам, хотя некоторые авторы утверждают обратное. Тем не менее, исходя из того, что Ом не употребляет этот термин в первом издании своей книги, Роджер Герц-Фишлер делает вывод о том, что этот термин, возможно, появился в первой четверти XIX века.Марио Ливио считает, что он получил популярность в устной традиции около 1830 года. В любом случае, этот термин стал распространён в немецкой математической литературе после Ома.

Расчёт относительного отверстия

Геометрическое относительное отверстие N{\displaystyle N} выражают в виде дроби:

N=Df′{\displaystyle N={D \over f’}},

где D{\displaystyle D} обозначает диаметр входного зрачка, а f′{\displaystyle f’} — заднее фокусное расстояние. Относительное отверстие принято обозначать соотношением двух чисел, написанных через двоеточие. При этом, первое число всегда принимается за единицу, например 1:5,6. В современной литературе более широкое распространение получило обозначение относительного отверстия в виде дроби с числителем f, например f/5,6. Для зеркально-линзовых объективов площадь входного зрачка рассчитывается по более сложному закону, поскольку его центральная часть экранирована. В этом случае диафрагма может иметь форму не круга, а кольца, и для нахождения диаметра входного зрачка необходимо реальный входной зрачок (кольцо) заменить при расчёте кругом эквивалентной площади. Диаметр найденного круга и будет являться искомым диаметром входного зрачка для применения в дальнейших расчётах.

Квадрат относительного отверстия называется светосилой и определяет соотношение яркости объекта и освещённости его изображения в фокальной плоскости.
Эффективное относительное отверстие вычисляется с учётом коэффициента светопропускания τ{\displaystyle \tau } оптической системы, учитывающего общую толщину стекла и количество границ воздух/стекло.
Коэффициент, снижающий прозрачность объектива, определяется по формуле:

τ=(1−P)n⋅(1−α)m{\displaystyle \tau =(1-P)^{n}\cdot (1-\alpha )^{m}},

где P{\displaystyle P} — доля света, теряемая при ;

n{\displaystyle n} — число поверхностей раздела воздух/стекло;

α{\displaystyle \alpha } — удельное поглощение света в 1 сантиметре стекла;

m{\displaystyle m} — суммарная толщина линз объектива в сантиметрах.

Для непросветлённых объективов τ{\displaystyle \tau } не превышает 0,65. Объективы с просветлением теряют не более 10% света при его прохождении и рассеянии.

Приведённые способы расчёта геометрического и эффективного относительного отверстия справедливы только при фокусировке объектива на «бесконечность». Для конечных дистанций знаменатель дроби увеличивается из-за выдвижения объектива, приводя к уменьшению относительного отверстия. Эффект особенно заметен при макросъёмке, когда сопряжённое фокусное расстояние может превосходить расчётное в два и более раз. В этом случае пренебрегать изменением относительного отверстия недопустимо и требуются поправки при расчёте экспозиции.

Золотое сечение и гармония в искусстве

Золотое сечение и зрительные центры

Некоторые из утверждений в доказательство гипотезы знания древними правила золотого сечения:

• Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.
• Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д. При обсуждении оптимальных соотношений сторон прямоугольников (размеры листов бумаги A0 и кратные, размеры фотопластинок (6:9, 9:12) или кадров фотоплёнки (часто 2:3), размеры кино- и телевизионных экранов — например, 4:3 или 16:9) были испытаны самые разные варианты. Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми»[источник не указан 3728 дней].
• Следует отметить, что сама пропорция является, скорее, эталонным значением, матрицей, отклонения от которой у биологических видов, возможно, вызваны приспособлением к окружающей среде в процессе жизни. Примером таких «отклонений» может служить морская камбала.

Один из типов мозаики Пенроуза

Примеры сознательного использования

Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий И. В. Жолтовский использовал золотое сечение в своих проектах.
Иоганн Себастьян Бах в своей трёхголосной инвенции E-dur № 6 BWV 792 использовал двухчастную форму, в которой соотношение размеров частей соответствует пропорциям золотого сечения. 1 часть — 17 тактов, 2 часть — 24 такта (небольшие несоответствия выравниваются за счёт ферматы в 34 такте)[источник не указан 953 дня].

Современными примерами применения золотого сечения может служить мозаика Пенроуза и пропорции государственного флага Того.

F-число

F-число Фарадея ( 96494 Кл), а0х — активность окисленной формы; aRed — активность восстановленной формы. На практике электродный потенциал часто принимают равным Е0, когда концентрации окисленной и восстановленной форм равны и не обязательно имеют единичную величину.
 

F и u — F; F-число Фарадея, равное 96500; z, — валентность иона; R — газовая постоянная, равная 8 315 дмс, Т — абсолютная температура.
 

К; п-число теряемых или приобретаемых электронов; F-число Фарадея, равное 96 500 кулонам;

Соединяя центр данного правильного многогранника с его вершинами, мы разложим его на F равных правильных пирамид, где F-число граней многогранника.
 

К-газовая константа, равная 8 314 джоуля; Т — абсолютная температура раствора; п-число теряемых или приобретаемых электронов; F-число Фарадея, равное 96 500 кулонам;

Здесь / — сила тока, мА; / — время генерации гидроксид-ионов, с; Ан — атомная масса бора; п 1-число электронов; F-число Фарадея.
 

R-универсальная газовая постоянная [ 8 314 Дж / ( К-моль) ]; Т — абсолютная температура; п — число электронов, принимающих участие в электродной реакции; F-число Фарадея ( 96493 Кл на моль электронов); QM.
 

Еа — стандартный электродный потенциал; R — универсальная газовая постоянная [ R 8 314 Дж / ( моль — К) ]; Т — абсолютная температура, К; F-число Фарадея ( / 96500 Кл); п — число молей электронов, принимаемых при превращении окисленной формы в восстановленную; а и а 0с — активность соответственно окисленной и восстановленной формы.
 

Здесь ф — стандартный электродный потенциал данного процесса — константа, физический смысл которой рассмотрен ниже; R — газовая постоянная; Т — абсолютная температура; г — число электронов, принимающих участие в процессе; F-число Фарадея; и — произведения концентраций веществ, участвующих в процессе в окисленной ( Ох) и в восстановленной ( Red) формах.
 

Падение потенциала в этой области составляет часть ( а) всего потенциала разряда и равно арк. Потенциальный барьер, тормозящий электрохимическую реакцию, снижается действием электрического поля электрода. Это снижение потенциального барьера равно по абсолютной величине срк / % где F-число Фарадея.
 

Под аналого-цифровой системой коммутации понимается комплекс оборудования, на вход которого поступают заявки на обслуживание от аналоговых абонентских терминалов, а на выходе имеются скоммутированные в соответствии с требованиями на установление соединения цифровые сигналы. Оптимизация аналого-цифровой системы коммутации сводится к такому выбору ее структурных параметров, чтобы при заданных исходных данных она обладала бы минимальной стоимостью. Исходными данными являются: Nc-емкость ( число входов) аналого-цифровой системы коммутации; Ah — матрица распределения внутристанционного потока нагрузки; п — качество обслуживания ( потери); F-число каналов в цифровом тракте ( зависит от типа системы передачи); с-стоимость компонентов системы. Предполагается, что стоимость эксплуатационных затрат и затраты на управляющие устройства слабо зависят от структуры системы, поскольку независимо от структуры системы параметры общего потока нагрузки и качество обслуживания сохраняются постоянными, а именно они в первую очередь влияют на указанные затраты.
 

Золотое сечение в науке

Общее сопротивление этой бесконечной цепи равно Фr.

Золотое число возникает в разных задачах, в том числе в физике. Например, бесконечная электрическая цепь, приведенная на рисунке, имеет общее сопротивление (между двумя левыми концами) Ф·r.

Отношение амплитуд колебаний и частот ~ Ф.

Существуют колебательные системы, физические характеристики которых (отношения частот, амплитуд и др.) пропорциональны золотому сечению. Самый простой пример — система из двух шариков, соединенных последовательно пружинами одинаковой жесткости (см. рисунок).

Полностью эти две задачи рассматриваются в книге «В поисках пятого порядка», глава «Две простые задачки». Более сложные примеры на механические колебания и их обобщения рассматриваются в этой же книге, в главе «Обобщения одной простой задачи по механике». В книге приведено много примеров проявления и применения золотого сечения в различных областях наук — небесной механике, физике, геофизике, биофизике, физической химии, биологии, физиологии.

Золотое сечение сильно связано с симметрией пятого порядка, наиболее известными трехмерными представителями которой являются додекаэдр и икосаэдр. Можно сказать, что всюду, где в структуре проявляются додекаэдр, икосаэдр или их производные, там в описании будет появляться и золотое сечение. Например, в пространственных группировках из Бора: В-12, В-50, В-78, В-84, В-90, …, В-1708, имеющих икосаэдрическую симметрию.
Молекула воды, у которой угол расхождения связей Н-О равен 104.7 , то есть близок к 108 градусам (угол в правильном пятиугольнике), может соединяться в плоские и трехмерные структуры с симметрией пятого порядка. Так в разреженной плазме был обнаружен Н+(Н₂0)₂₁, который представляет из себя ион Н₃0+, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра. В 80-х годах XX века были получены клатратные соединения, содержащие гексааквакомплекс кальция, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра. Есть и клатратные модели воды, в которых обыкновенная вода отчасти состоит из молекул воды, соединенных в структуры с симметрией пятого порядка. Такие структуры могут состоять из 20, 57, 912 молекул воды.

Литература

Гордийчук, И. Б. Справочник кинооператора / И. Б. Гордийчук, В. Г. Пелль. — М. : Искусство, 1979. — 440 с. — 30 000 экз.

Е. А. Иофис. Фотокинотехника / И. Ю. Шебалин. — М.,: «Советская энциклопедия», 1981. — С. 228. — 447 с. — 100 000 экз.

Н. Д. Панфилов, А. А. Фомин. Краткий справочник фотолюбителя / Н. Н. Жердецкая. — М.: «Искусство», 1985. — С. 179—184. — 367 с. — 100 000 экз.

Фомин А. В. § 4. Фотографические объективы // Общий курс фотографии / Т. П. Булдакова. — 3-е. — М.,: «Легпромбытиздат», 1987. — С. 124—130. — 256 с. — 50 000 экз.

Хокинс Э., Эйвон Д. Фотография: Техника и искусство / А. В. Шеклеин. — М.: «Мир», 1986. — С. 45—55. — 280 с. — 50 000 экз.

Шаг третий. Как диафрагма влияет на экспозицию

Теоретически, вместе с изменением радиуса диафрагменного отверстия изменяется и экспозиция. Чем шире будет открыто отверстие диафрагмы, тем больше света попадет на светоприеменик. Об этом мы уже не раз сегодня говорили. И, стало быть, чем больше света попадает на матрицу, тем светлее получится снимок. Для того, чтобы лучше себе представить всё это, посмотрите внимательно вот на эту серию снимков. Все они были сделаны с различными значениями диафрагмы. Остальные настройки экспозиции были постоянными: выдержка 1/400 секунды, светочувствительность – 200 единиц ISO.  Менялась только диафрагма: f/2. f/2,8. f/4. f/5,6. f/8. f/11. f/16. f/22.

Тут так же обратим ваше внимание и на то, что главная творческая задача диафрагмы – это ее влияние на глубину резко изображаемого пространства

Шаг второй. Шкала диафрагмы

Шкала диафрагмы – это ряд  значений диафрагмы по возрастающей. Шкала диафрагмы обычно бывает нанесена на оправу объектива, а так же мы можем видеть ее на дисплее фотокамеры. Размер отверстия диафрагмы обычно выражается в виде знаменателя дроби и обозначается символом «f». То есть «f/число». Знаменатель этой дроби как раз и указывает, насколько широко в данный момент открыто диафрагменное отверстие. А эта ширина, как мы уже говорили сегодня, существенным образом и влияет на экспозицию. Но кроме экспозиции, размер диафрагменного отверстия так же влияет и на глубину резко изображаемого пространства

Тут важно знать, что чем число, которым обозначено то или иное значение диафрагмы, меньше – тем шире диаметр отверстия диафрагмы. Проще говоря, диаметр отверстия диафрагмы, обозначенной  f/8 меньше, чем, допустим,  диафрагма  f/4

У некоторых начинающих фотографов это, возможно, может вызвать путаницу: как же так? Число маленькое, а диаметр отверстия – большой? Ответ на этот вопрос  довольно простой. Пока скажем, что всё дело тут в математике. Но об этом чуть позже.

А пока мы расскажем вам о стандартной диафрагменной шкале. Вот этот ряд чисел: f/1,4. f/2. f/2,8. f/4. f/5,6. f/8. f/11. f/16. f/22.

Самое важное, что нужно знать об этой шкале – это то, что каждая ступень, каждый шаг этой шкалы, каждый переход от меньшего числового значения к большему уменьшает диаметр отверстия диафрагмы ровно в два раза. А это, соответственно, значит, что пропускает на матрицу ровно на 50% меньше света

Практически на всех объективах вы найдете надпись в виде соотношений значений чисел. Ну, например, 1:2. Что это означает? Это означает то, что диаметр отверстия данного объектива  в два раза меньше его фокусного расстояния. Но большинство из современных фотокамер и объективов сегодня имеют не только стандартные значения диафрагмы, но и промежуточные. Проще говоря, допустим, если шаг настройки равен 1/3 ступени, то между значениями диафрагмы f/4 и  f/2,8 будут располагаться и еще несколько ее значений, а именно f/3,2 и  f/3,6. Для чего это нужно? В первую очередь для того, чтобы иметь возможность более точной настройки экспозиции. А так же и других нужд, о которых мы поговорим с вами чуточку попозже.

А сейчас перейдем к вещам посложнее. Скажем сразу: если то, о чем мы сейчас будем говорить, покажется вам не очень понятным и недоступным, не бойтесь перейти к следующему разделу. Мы же пока попытаемся разобраться, почему же, все-таки, при переходе от меньшего значения диафрагмы к большему сквозь объектив фотоаппарата света проходит именно в два раза меньше.

Давайте рассмотрим этот вопрос на одном примере. Представим, что у нас с вами в руках объектив с фокусным расстоянием 50 миллиметров и с диафрагмой f/2. Первым делом рассчитаем диаметр самого отверстия диафрагмы. Для этого нам придется 50 миллиметров разделить на 2. В итоге получаем 25 миллиметров. Далее. Ищем радиус этого отверстия, то есть половину диаметра. Радиус у нас, стало быть, составляет 12.5 миллиметров. Теперь по известной формуле S = пи * R2 (число пи умножить на радиус в квадрате)  нам нужно узнать площадь этого отверстия. В данном  случае эта площадь составляет у нас 490 квадратных миллиметров.

А теперь давайте сделаем такие же расчеты для этого объектива при другом значении диафрагмы. При f/2,8 диаметр диафрагменного отверстия будет  17,9 миллиметров, радиус, соответственно,8,95 миллиметров,  а площадь – 251,6 квадратных миллиметров. Не нужно быть великим знатоком для того, чтобы понять, что вторая площадь в данном случае практически вдвое меньше, чем первая

На то, что число 2 является приблизительным, обращать внимание не стоит. Дело в том, что округление диафрагменного числа сделано до первого десятичного знака

А если расчеты проводить без округлений, то, как раз ровно 2 и получится.

Литература

• Аракелян Г. Б. Математика и история золотого сечения. — М.: Логос, 2014, 404 с. — ISBN 978-5-98704-663-0.
• Васютинский Н. А. Золотая пропорция. — М.: Молодая гвардия, 1990. — 238c. — (Эврика).
• Власов В. Г. Новый энциклопедический словарь изобразительного искусства: В 10 т. — Т.3. — СПб.: Азбука-Классика, 2005. — С.725-732.
• Власов В. Г. Искусство России в пространстве Евразии. — Т.3. Классическое искусствознание и «русский мир». — СПб.: Дмитрий Буланин, 2012. — С.156-192.
• Мазель, Л.А. Опыт исследования золотого сечения в музыкальных построениях в свете общего анализа форм // Музыкальное образование. – 1930. – № 2. – С. 24-33.
• Сабанеев Л. Л. Этюды Шопена в освещении закона золотого сечения. Опыт позитивного обоснования законов формы // Искусство. — 1925. — № 2. — С. 132—145; 1927. — № 2-3. — С. 32-56.
• Шмигевский Н. В. Формула совершенства // Страна знаний. — 2010. — № 4. — С.2-7.
• Русский перевод в

Roger Herz-Fischler. A Mathematical History of the Golden Number. — Courier Corporation, 2013. — 228 с. — ISBN 9780486152325.

Способы определения

Число e может быть определено несколькими способами.

• Через предел:

  e=limx→∞(1+1x)x{\displaystyle e=\lim _{x\to \infty }\left(1+{\frac {1}{x}}\right)^{x}} (второй замечательный предел).

  e=limn→∞nn!n{\displaystyle e=\lim _{n\to \infty }{\frac {n}{\sqrt{n!}}}} (это следует из формулы Муавра — Стирлинга).

• Как сумма ряда:

  e=∑n=∞1n!{\displaystyle e=\sum _{n=0}^{\infty }{\frac {1}{n!}}} или 1e=∑n=2∞(−1)nn!{\displaystyle {\frac {1}{e}}=\sum _{n=2}^{\infty }{\frac {(-1)^{n}}{n!}}}.

• Как единственное число a{\displaystyle a}, для которого выполняется

  ∫1adxx=1.{\displaystyle \int \limits _{1}^{a}{\frac {dx}{x}}=1.}

• Как единственное положительное число a{\displaystyle a}, для которого верно

  ddxax=ax.{\displaystyle {\frac {d}{dx}}a^{x}=a^{x}.}

Диафрагма.

 Количество поступающего в аппарат света можно регулировать, изменяя степень освещенности пленки (матрицы). Достигается путем изменения отверстия объектива или диафрагмы.

       Диафрагма представляет собой заслонку, состоящую из нескольких лепестков образующих в центре объектива примерно круглое отверстие. 

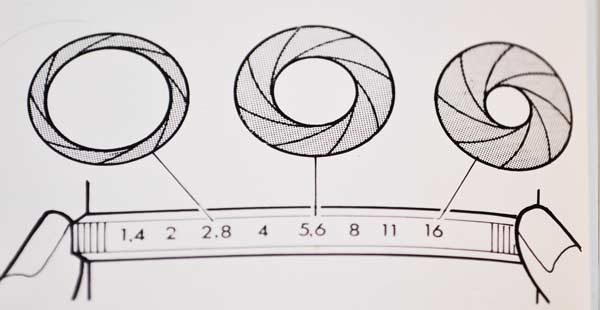
     Диаметр отверстия регулируется. Регулировка шкалы диафрагмы на современных камерах расположена не на объективе, а в самом фотоаппарате, обычно тот же диск что регулирует выдержку или диск рядом. Она имеет стандартную шкалу значений. 1;  1.4;  2;  2.8;  4;  5.6;  8;  11; 16;  22  или обозначается так 1/2.8;    1/4;  …… 1/11 и т.д.  Каждое следующее больше предыдущего в 1.4 раза, поворот диска на одно деление от большего числа к меньшему соответствует увеличению площади отверстия объектива в 2 раза. То есть чем больше число, тем меньше площадь дырки диафрагмы.    Например, при диафрагме 11 площадь меньше чем при диафрагме 8 и, следовательно, объектив пропускает в 2 раза меньше света. Обычно перед значениями диафрагмы  ставится буква F.

    Числа определяющие площадь отверстия называются значениями диафрагмы или просто диафрагмой..

   Различие между значениями часто называют ступенями или шагами, например, меняя диафрагму с 11 на 4 мы увеличиваем(открываем отверстие) экспозицию на 3 ступени, шага. 11 —  8 — 5.6 – 4

   При одном и том же значении диафрагмы любой объектив пропускает одинаковое количество света, но размер самого отверстия может быть разным в зависимости от фокусного расстояния объектива.

    Чем больше фокусное расстояние объектива, тем больше диаметр отверстия при одной и той же диафрагме. Но интенсивность света падающего на пленку или матрицу одна и та же.

Итак, величину экспозиции можно регулировать с помощью либо выдержки, либо диафрагмы.

Диафрагму важнее всего учитывать при постройке экспозиции в художественной фото т.к. она влияет на глубину резкости изображаемого пространства (ГРИП), об этом ниже. В съемке например спортивных сюжетов важнее всего выдержка т.к. нужно часто остановить движение.

Исчисляемые и неисчисляемые существительные

Исчисляемые существительные мы можем посчитать: six jobs (шесть работ), many offers (много предложений).
Неисчисляемые (несложно догадаться) посчитать невозможно, они не образуют множественного числа. Как и в русском языке, мы не употребим слова: музыка, кровь, вода или золото (music, blood, water, gold) во множественном числе.
Хотя, так же как и в русском, в зависимости от контекста, возможны варианты: воды Атлантики — waters of Atlantic, смешение кровей — bloods mixing.

Некоторые существительные могут быть как исчисляемыми так и неисчисляемыми. Определить это несложно из контекста: I bought a paper. — Я купил газету. Газета — исчисляемое существительное. Газеты мы можем посчитать.
А вот другой пример:I bought some paper. — Я купил бумагу. Бумага — неисчисляемое существительное. Бумага — это «материал», который мы посчитать не можем, её возможно посчитать только в листах, рулонах и т.д.

Следующие существительные имеют одинаковую форму единственного и множественного числа, т.е. они совпадают:
fish (рыба — рыбы (но: fishes — виды рыб или рыбки),
deer (олень — олени),
sheep (овца — овцы),
fruit (фрукт — фрукты (но: fruits — виды фруктов),
aircraft (самолёт — самолёты) и др.

Есть также существительные, которые употребляются только во множественном числе:
clothes — одежда,
police — полиция
cattle — скот
pyjamas — пижама
trousers — штаны
breeches — бриджи
glasses — очки
spectacles — это тоже очки
scissors — ножницы
goods — товары, (часто переводится на русский в единственном числе — товар)
holidays — каникулы (есть и единственное число — holiday, но это уже праздник)
customs — таможня
jeans — джинсы
tights — колготки
shorts — шорты и др. (почти как в русском языке).

Но раз есть существительные, которые употребляются только во множественном числе, то конечно есть и те, которые употребляются только в единственном:
advice — совет,
furniture — мебель,
hair — волосы,
information — информация,
knowledge — знание,
money — деньги (а у нас наоборот только во множественном),
trouble — проблема

К этому списку можно добавить ещё несколько слов, которые несмотря на конечную -s употребляются в единственном числе: physics, mathematics, optics, phonetics, politics и им подобные.

Особняком стоят такие слова как news — новости, оно считается существительным множественного числа (plural), но в предложении употребляется как единственное (singular). На русский переводится по смыслу множественным или единственным числом:
This was news to me. — Это было новостью для меня.
What’s the news? — Что новенького? (или: Какие новости?)

К «новостям» можно добавить ещё несколько подобных слов у которых единственное число ничем не отличается от множественного (хотя, в зависимости от контекста, тоже возможны варианты):
means = средство — средства
barracks = казарма — казармы (но: barrack — барак)
crossroads = перекрёсток — перекрёстки (но иногда мы попадаем и на «crossroad»)
headquarters = штаб — штабы
series = серия — серии
species = вид, разновидность — виды разновидности
works = завод, фабрика — заводы, фабрики

А теперь проверьте себя.
Выберите подходящий вариант :

1. The apartment is empty. We haven’t got any furnitures/furniture yet.
2. I had trouble/troubles with my car this morning.
3. Ann has got very long black hair/hairs.
4. I didn’t know what to do. I asked Jack for advice/advices.

К оглавлениюКлючи к упражнениямСлушатьГрамматика в халатике

Открытые проблемы

• Неизвестно, является ли число e{\displaystyle e} элементом кольца периодов.
• Неизвестна мера иррациональности ни для одного из следующих чисел: π+e,π−e,π⋅e,πe,πe,eπ2,ee,2e.{\displaystyle \pi +e,\pi -e,\pi \cdot e,{\frac {\pi }{e}},\pi ^{e},e^{\pi ^{2}},e^{e},2^{e}.} Ни для одного из них неизвестно даже, является ли оно рациональным числом, алгебраическим иррациональным или трансцендентным числом. Следовательно, неизвестно, являются ли числа π{\displaystyle \pi } и e{\displaystyle e} алгебраически независимыми..
• Неизвестно, является ли первое число Скьюза eee79{\displaystyle e^{e^{e^{79}}}} целым числом.

Примечания

1. ↑
2. Mario Livio, The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number
3. Boyer, Carl B. A History of Mathematics. — Second Edition. — John Wiley & Sons, Inc., 1991. — P. 50. — ISBN 0-471-54397-7.
4. , p. 168.
5. , p. 6-7.
6. , p. 169.
7. , p. 7.
8. , p. 169-170.
9. .
10. Ковалев А.Н. В поисках пятого порядка. — 2017. — 374 с. — ISBN 978-5-4485-3753-0.
11. Современная Кристаллография / под ред. Вайнштейна Б. К.. — Т.2. — М.: Мир, 1979.
12. Holland P. M. Casteiman A. W. A model for the formation and stabilization of chorqed water cluthrates // J. Chem. Phys.. — 1980. — Т. 72, № 1(11). — С. 5984.
13. Электромагнитные поля в биосфере. — Сборник трудов конференции, Т.2. — М., 1984. — С. 22.
14. Зенин С.В. Структурированное состояние воды как основа управления поведением и безопасностью живых систем. — Диссертация докт. биол. наук. — М., 1999.